イスラエルのバル＝イラン大学がべき乗スケーリングの深層学習への応用を実証！

はじめに
　イスラエルのバル＝イラン大学が、人工知能の分野における2つの課題（①モデルに必要なデータセットの大きさの推定、②限られた時間、データセット内でいかに信頼できる意思決定を可能にするか）に対して、1世紀前に導入された物理的概念であるべき乗測スケーリング（鉄バルクの冷却プロセスにおける磁石の形成を説明するために利用された概念）を利用することで解決しました。
　実験では慎重な最適化手順と徹底的なシミュレーションによって、深層学習へのべき乗則スケーリングの物理的概念の有用性が実証しました。

概要

　これまで、AI分野では、以下の二つの課題が指摘されてきました。

（a）必要なテスト精度を達成するために必要なデータセットサイズの事前推定。
例）99％の成功率で新しい数字を予測する前に、何桁の手書き数字を学習する必要があるか？
（b）限られた数の例の下での信頼できる意思決定の達成。

　イスラエルのバル＝イラン大学が、物理学における中心的な概念のひとつであるべき乗測のスケーリングが、慎重な最適化と徹底的なシミュレーションによって、この課題の解決に有効であることを明らかにしました。べき乗測スケーリングは、すでに地震のタイミングと規模、インターネットトポロジーとソーシャルネットワーク、株価の変動、言語学における単語の頻度、脳活動における信号の振幅など様々な分野で応用されており、今回の研究でAI分野にも応用できることがわかりました。
　さまざまな動的ルールとネットワークアーキテクチャを管理するべき乗則のスケーリングにより、調査されたさまざまな分類または決定問題間での分類と階層の作成が可能になります。

詳細

●物理学とAIの関係性
　相転移や臨界現象は、20世紀後半から統計力学の中心的な研究対象となってきました。二次相転移の臨界点付近の熱力学的性質は、系の次元性に応じて、べき乗スケーリングなどを用いて説明されてきました。
　ディープラーニングアルゴリズムは、宇宙物理学の分類問題や高エネルギー物理学のデータ解析から、ノイズ光学のイメージングや位相遷移の学習特性に至るまで（物理学の実験データの解析を含む）これまでにないほど多くのアプリケーションで有用であることがわかっています。今回の研究では、深層学習アルゴリズムが臨界物理システムと漸近的に類似した振る舞いをすることを示しています。
　ディープラーニングの基本的なタスクは教師付き学習であり、多層ネットワークが訓練データベースに基づいて、入力データに対して正しい出力ラベルを生成するように学習します。選択されたフィードフォワードネットワークの重みは、コスト関数を最小化するように勾配降下ベースのアルゴリズムである誤差逆伝播アルゴリズムを使用して調整されます。これらによって、現在の出力と所望の出力の間のミスマッチが定量化されます。アルゴリズムの性能は、訓練中に観測されなかったデータセットで測定されたテスト誤差を用いて推定されます。検定誤差は、情報量の増加とデータセットサイズの増加に伴って減少し、十分に複雑なネットワークでは漸近的に消失すると予想されます。べき乗スケーリングによる検定誤差の消失が、今回の研究の焦点です。

●研究
　望ましい検定精度を達成するために必要なデータセットサイズを事前に推定します。べき乗スケーリング現象のロバスト性は、1つのエポックと多数のエポック（＝各テストデータが訓練されたネットワークに提示される回数）、およびいくつかの隠れ層と重みについて検討されました。
　1つの訓練エポックで最適化されたテスト誤差の結果は、多数のエポックで構成される最先端のアルゴリズムに近接しており、限られた例数の下での迅速な意思決定に重要な意味を持ちます。現実では多数のエポック数で訓練することが困難であるため、高度な学習アルゴリズムとそのリアルタイム実装との間に生じる性能のギャップを、1つのエポックのみに基づいて最適な性能を達成することによって対処することができるというのが今回の研究の着目点です。
　様々な学習タスク、データセット、アルゴリズムから得られるべき乗スケーリング、指数、定数係数の比較は、それらの複雑さを測定するための定量的な理論的枠組みのベンチマークを確立することが期待されています。
　
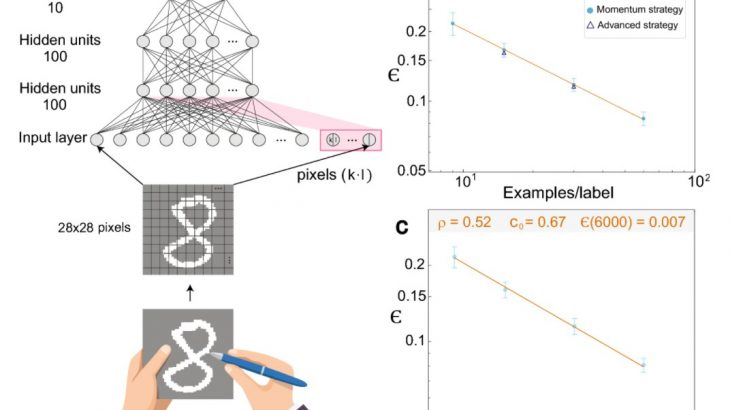
多くのエポックでのテストエラーのべき乗則スケーリング

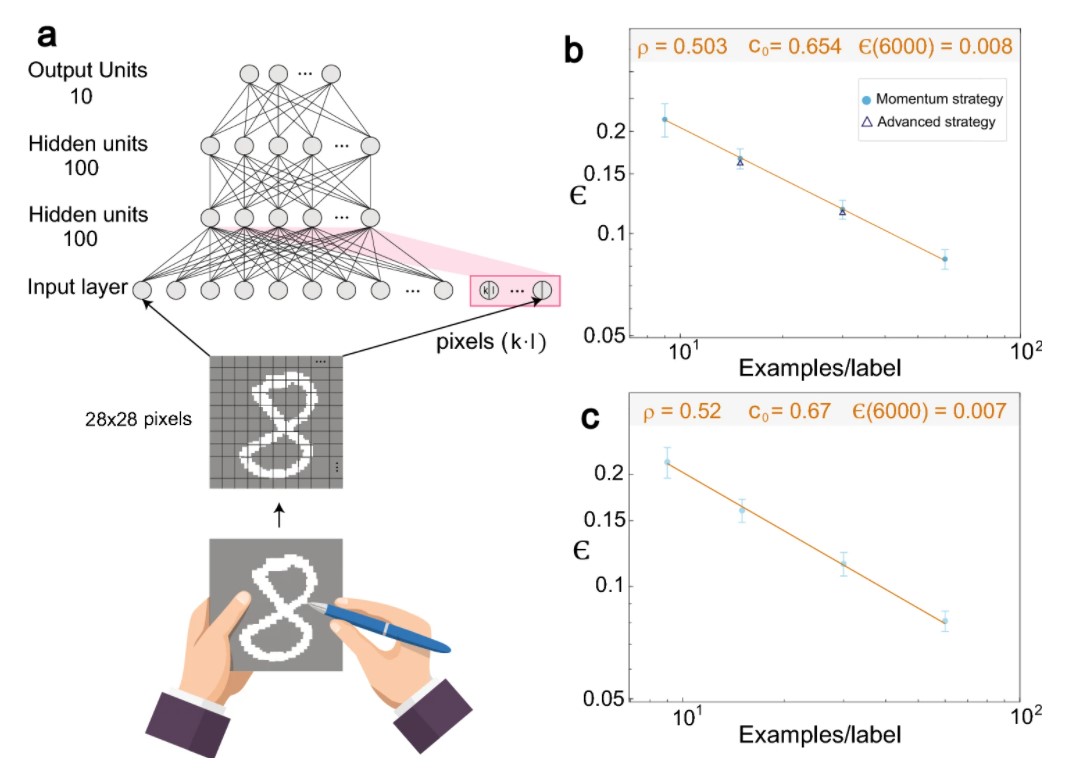
（a）MNIST手書き数字のスキーム。これはデジタル化され、入力クロス（赤い背景）を含むトレーニング済みネットワークに供給されます。
（b）（a）のアーキテクチャを使用して、9、15、30、および60のデータ/ラベルと50のサンプルから得られたそれらの標準偏差を含む限られたデータセットに対して最適化されたテストエラーϵ。
(c) Nc = 50のテストエラー