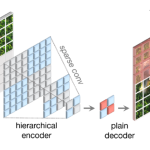
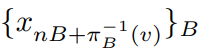ディープニューラルネットワークは近年まで非常に複雑な関数であるため学習がうまくいくとは思われていませんでした。近年GPUの発達などで学習が可能になりましたが、学習がうまくいく理由について明らかになってはいませんでした。2019年に米デューク大学の研究チームが行った、ディープニューラルネットワークの学習がSGDでうまくいく理由を調査した論文を解説します。
概要
・研究の背景
ディープニューラルネットワークの学習においてSGDを利用すると経験的にうまくいくことが知られているが、なぜ複雑なニューラルネットワークを大域最適解に導くかがよくわかっていない。
・研究の目的
SGDが非凸最適化問題における大域極小値に収束する理由を明らかにする。
・研究の成果
①多くのディープニューラルネットワークで学習損失がゼロに到達すること(⇔学習がうまくいっていること)
②学習損失がゼロになっている場合、SGDはstar-convex path を通過している(⇔star-convex path を通過する場合、学習がうまくいく。)
詳細
論文の内容を詳細に解説します。
イントロダクション
ディープラーニング初期(1980年代)は、コンピュータリソースの制約もあり学習不可能だと考えられていました。しかし、2015年ごろからGPUの利用が普及することで学習が可能となり、現実世界のデータセットに対しても対応することが可能となりました。
SGDは初期から利用され、近年はその変異系としてAdamやAdagrad などが利用されるようになっています。近年では、SGDが①鞍点から逃れられること、②局所極小値から逃れられることがわかってきました。それだけでなく、様々なディープニューラルネットワークの学習損失をゼロにすることが可能であることもわかってきました。この現象を理解するうえで困難なことは、①ディープニューラルネットワークの複雑な勾配は完全に解析的に理解することができないこと、②SGDのランダムな数値が複雑な勾配を収束する特徴づけを困難にしていることなどがあげられます。
これらの難点を超えて理解するために、研究チームは以下のふたつの特性に注目しています。
①SGDがニューラルネットワークの損失をゼロにすることができるという事実は、すべてのデータサンプル上の非負損失関数は大域極小値を共有していること
②ゼロ損失に到達しているときSGDは、star-convex path を通過していること
問題の設定と準備
SGDの特性を理解するうえで、定義と問題の設定を明示します。
まず、SGDの式は以下のように示されます。
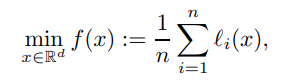
n:学習データサンプルの総数
li :各バッチの番号
⇒非凸最適化問題となる
上記の式を踏まえ、以下の仮定を設定します。(なお、以下の設定仮定は非凸最適化の場合、一般的仮説となります。)
仮定1(非凸最適化の場合は、一般的仮説)
1.連続してデータが異なる場合、勾配がリプシッツ連続となる
2.すべての値に対して、損失が0以上となる
また、以下の観察が得られています。
観察1(ディープラーニングの大域極小値)
ある変数xのときに、損失がゼロに到達する。
そのため、あるxはすべての個々の損失に対して共有する大域極小値であるといえる。
より公式化すると、ある損失に対する極小値を導く集合であるXは、非空ではあり有界であるといえる。
大域極小値へのアプローチ
以下の設定で、学習させてSGDの効果を確認します。
学習設定
モデル:①MLP、②Alexnet、③InceptionNet
データ:Cifar10
損失関数:クロスエントロピーロス
最適化関数:SGD
学習率:0.01⇒MLP、Alxenet 0.1⇒InceptionNet
ミニバッチサイズ:128
エポック:学習損失がゼロになるまで十分な回数
使用しない工夫:モーメンタム、重み減衰、ドロップアウト、バッチノーマライゼーション
その他:各イテレーション後の重みパラメータを記録する
学習成果と学習経路
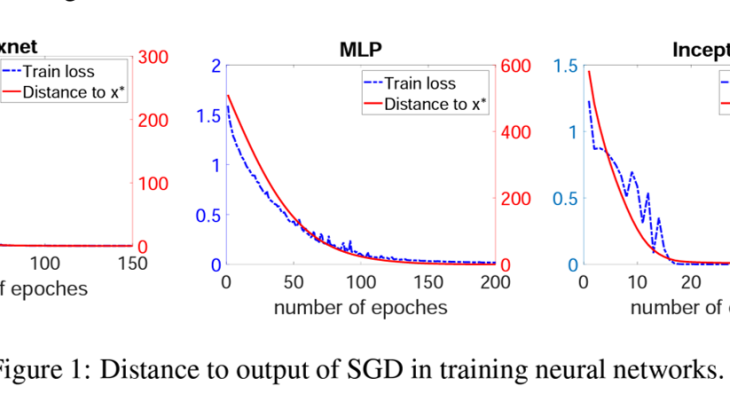
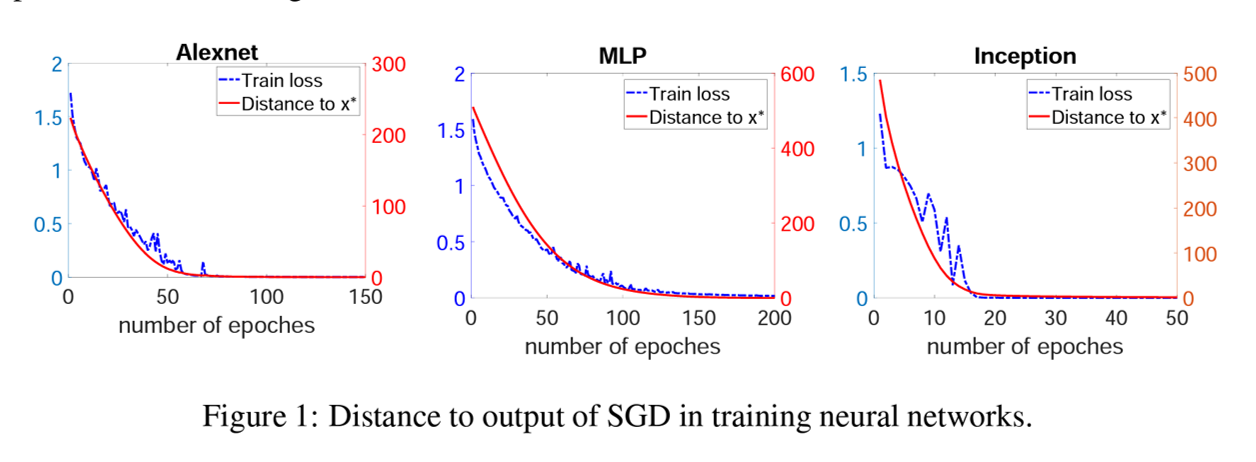
重みパラメータと最終出力値の間のユークリッド距離がエポックごとに徐々に小さくなっていることがわかります。つまり、大域極小値xへのアプローチが安定していることを意味しています。
star-convex path
star-convex pathへの知見と、SGDの収束の理論的実装を確立します。star-convex pathは以下の式で表されます。
![]()
x∗:大域極小値の解
h():なめらかな関数で、x において star-convex といえる。
star-convex は、基準点xとグローバル最小化子x ∗の間の凸性として直感的に理解できます。 このような特性により、負の勾配−∇h(x)が最小化のために目的の方向x ∗ −xを指すことが保証されます。
定義1
以下を満たすときに、エポックごとにSGDによって生成される経路を、epochwise star-convex といいます。
![]()
B=0, 1, … のエポック
最適化経路に関するアルゴリズムと損失関数の間の相互関係に特徴づけられます。
理論1(エポックごとに距離を低減する)
上記の仮説1が満たされるとき、いかが満たされます。
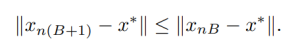
このとき、SGDによって生成される変数シークエンスは、エポックごとに大域極小値に向かっていることを示しています。
理論2(最小化サブシークエンス)
1.以下の対応する損失関数に対して、最小化シークエンスとなる。
![]()
これらの理論から、サンプリングによってもたらされるランダム性を超えて、SGDによってすべての個々のデータが大域解に到達する方向にむかうことを保証します。
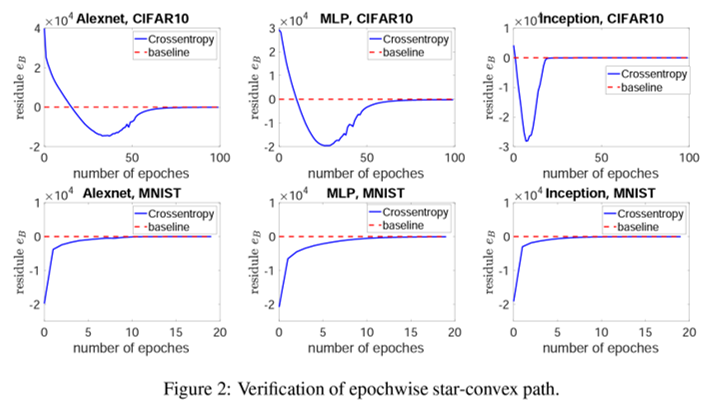
SGDの star-convex path の検証
マイナスからゼロに向かっている経路がstar-convex path を示しています。
Cifar10の方が複雑なため、数回のエポック後に経路に入っていることがわかります。
(対して、MNISTではすぐにstar-convex path にはいっています。)
大域極小値への収束
エポックレベルで、SGDによる変数シークエンスは大域極小値へ向かうことが明らかにされましたが、これはまだイテレーションレベルで保証しているわけではありません。
イテレーションレベルでのstar-convex path
SGDの収束を正規化することで、十分に保証することができます。
理論3 大域極小値への収束
仮説1に従い、学習率がn<1/Lのとき、イテレーションレベルでのstar-convex pathに従うと仮定した場合、SGDが大域極小値へ向かうことが保証されます。 すべてのデータサンプルに対して、損失関数の大域極小値が共有されることにより、保証されます。 ただし、この理論3における収束結果は、同一学習率に基づいています。学習率が低減していく手法では全く異なる可能性があることに注意が必要となります。
系1(分散の消失)
定理3と同じ設定で、反復kが無限大になると、SGDによってサンプリングされた確率的勾配の分散はゼロに収束します。
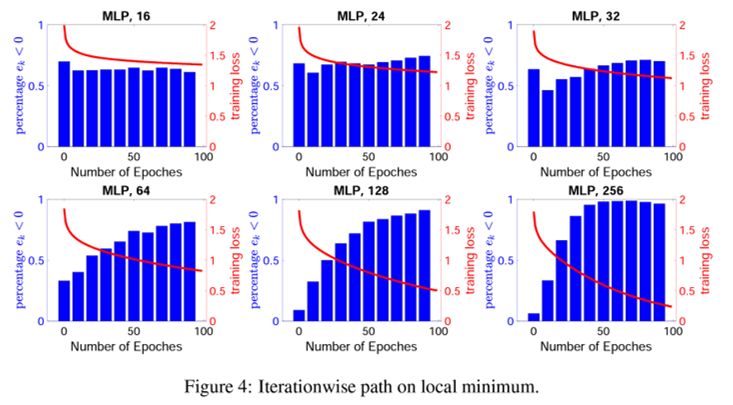
以下は、イテレーションレベルでもパスを通ることを示した図
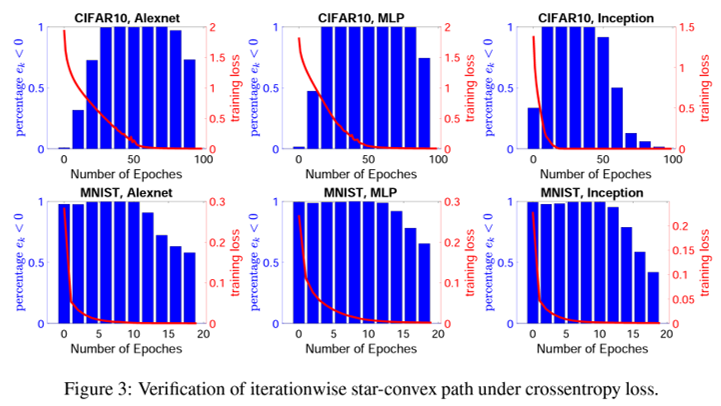
一方で、損失が0にならない場合は、star-convex path を満たす回数が減ることを以下では示している。
今回の証明手法について
今回の証明手法は、今後の証明に役立つ手法であると研究チームは考えています。
手順1)各サブシーケンスのすべての限界点が共通のグローバル最小化子であることを示す。
手順2)各サブシーケンスに固有の限界点があることを証明する。
手順3)これらすべてのサブシーケンスが、共通のグローバル最小化である同じ一意の限界点を共有することを示す。
結論
本論文では、SGDの最適化パスについて画期的な star-convex path を提案し、さまざまな実験で検証が行われました。このような特性に基づいて、SGDがエポックレベルで大域極小値に近づくことが示されました。
次に、イテレーションレベルでさらに調べ、学習時の大部分で上記の特性が満たされていることを実験的に示しました。