Facebookによる不完全情報ゲームに初めて対応したモデル『ReBeL』を紹介！

はじめに
　Facebookの研究チームが汎用性のある強化学習＋探索モデルとして新たにReBeLを発表しました。これまで完全情報ゲーム（囲碁やチェス、将棋など）では、AlphaZeroに代表される強化学習＋探索モデルは優秀な結果を残していましたが、不完全情報ゲーム（ポーカーなど）では期待通りの結果を残すことはできませんでした。今回発表されたReBeLは不完全情報ゲームでも優秀な結果を残しただけでなく、汎用性がたかく幅広いゲームに柔軟に応用できます。そのため研究チームは、ReBeLは汎用AIアルゴリズムへの大きな第一歩としています。

現況・課題

完全情報ゲームと不完全情報ゲーム

　これまで完全情報ゲームでは、強化学習＋探索モデルは良い結果を残してきました。しかし、不完全情報ゲームではあまりいい結果を残すことができませんでした。これはアルゴリズムが各手のもつ確率を踏まえて手の価値を変動させるということがうまくできていなかったためです。
　完全情報ゲームと不完全情報ゲームの大きな違いのひとつに、この手の価値を変動させる必要の有無という点にあります。完全情報ゲームにおいては常に良い手は良い手といえますが、不完全情報ゲームでは相手の手がわからない以上、同じ手でも自分の手が良い手なのかどうかを決定することはできず、限られた情報をもとに変更する必要があります。

不完全情報ゲームでの均衡

　不完全情報ゲームにおいて、一般的なアルゴリズムはナッシュ均衡となる選択することで利得を高くしようとするとします。実際、相手もナッシュ均衡になる選択肢を選んでいる場合、アルゴリズムは最大の利得を得ることができます。しかし、相手がナッシュ均衡とはならない選択を選んでくることは多々あります。その場合、アルゴリズムは相手がナッシュ均衡を選択するとおもっているので結果として本来ならより有利になる手があっても選べず、また不利になる手でも選択してしまいます。
　具体的に、じゃんけんで考えてみます。例えば、普通のじゃんけんでナッシュ均衡となる戦略はすべての手を均衡（１／３ずつ）に出すことであることが知られています。しかし、相手がそうした戦力を選ばず、常にひとつの手を出し続けるという戦略を選んでいるとします。この場合、そのことに気づいたプレイヤーであれば常に勝ち続ける手を選ぶという選択ができますが、ナッシュ均衡を選択するアルゴリズムはかわらず均等に手を選ぶため、勝ち越すことはできません。このように相手が何をだそうとしているのか、を推測してそれに対応した手を選択することが重要であることがわかります。
　ReBeLは、こうした相手が何を選択しようとしているのか、ということをうまく組み込むことで様々な不完全情報ゲームにも対応できる汎用性の高いモデルになりました

ReBeL（Recursive Belief-based Learning）

　基本的に完全情報ゲームで優れた成果を残したAlphaZeroに基づいてReBeLは構成されています。ReBeLの特徴は、ゲームの現在の状態について各プレーヤーが持っている可能性がある異なる信念の確率分布——公共信念状態（PBS：a public belief state ）——を考慮して決定を下します。（例えば、ReBeLは、ポーカーの対戦相手が敵（この場合、ReBeL）がエースのペアを持っていると考えている可能性を評価できます。）このことで、ReBeLは不完全情報ゲームを完全情報ゲームと同じように扱うことができます。そのため、ReBeLは二人対戦のゼロサムゲームであれば、完全・不完全を問わずどのようなゲームにも適応できます。

公共信念状態（PBS：a public belief state ）

　不完全情報ゲームは、見方を変えると完全情報ゲームの連続体とみなすことができます。論文では、トランプを使った不完全情報ゲームの例で説明されています。

基本ルール
①プレーヤーは、各自カードを一枚引きます。
②フォールド、コール、レイズの3つのアクションから順番に選択します。

修正したルール
①公平な「審判」だけが各自のカードを見ることができます。（プレイヤーはみることができません。）
②プレイヤーは、審判に対してカードに応じて特定の行動を取る確立がどれくらいあるかを発表します。
③審判は、プレイヤーから提示された確率分布に従って、プレイヤーに代わって行動を選択します。

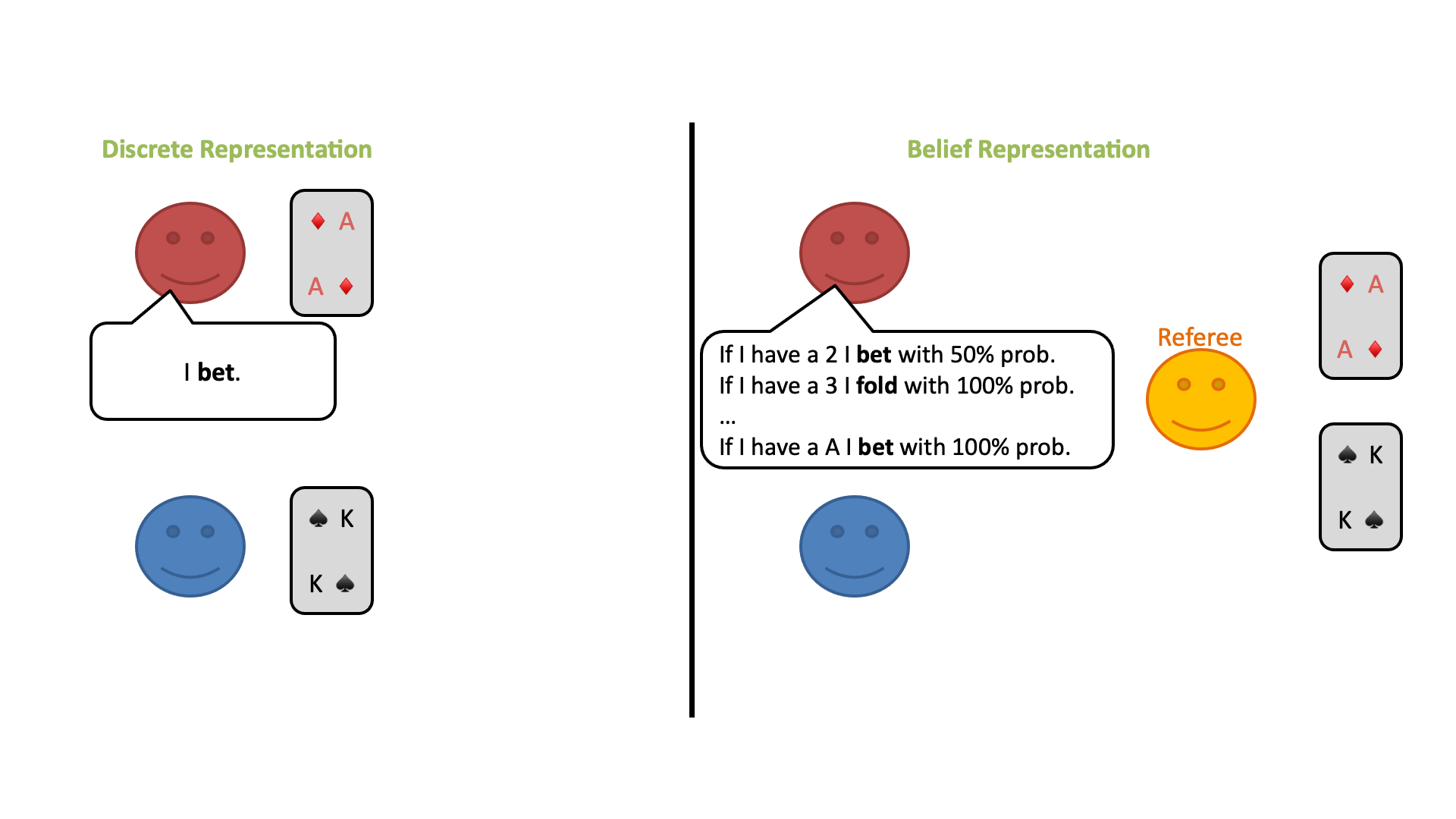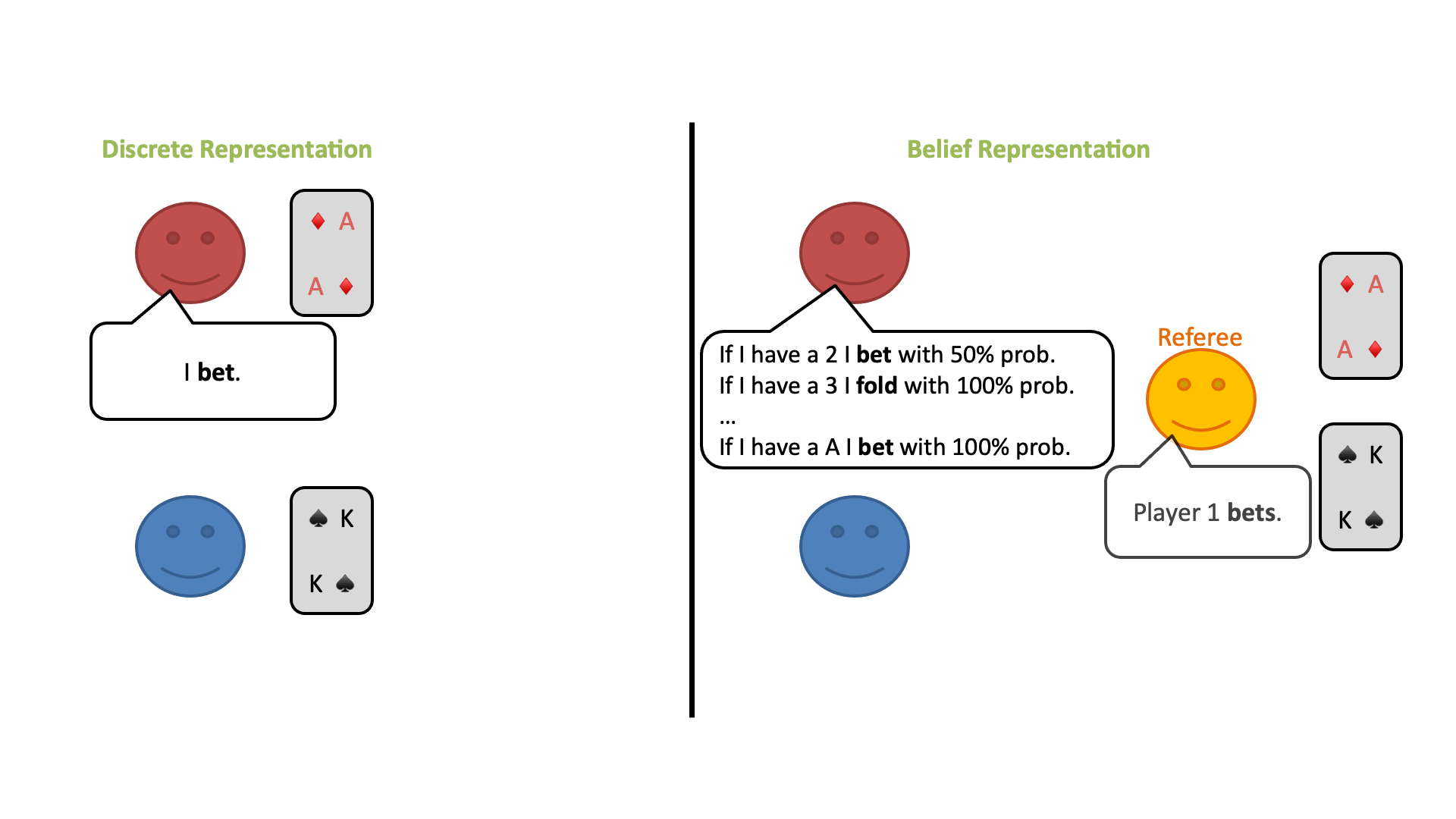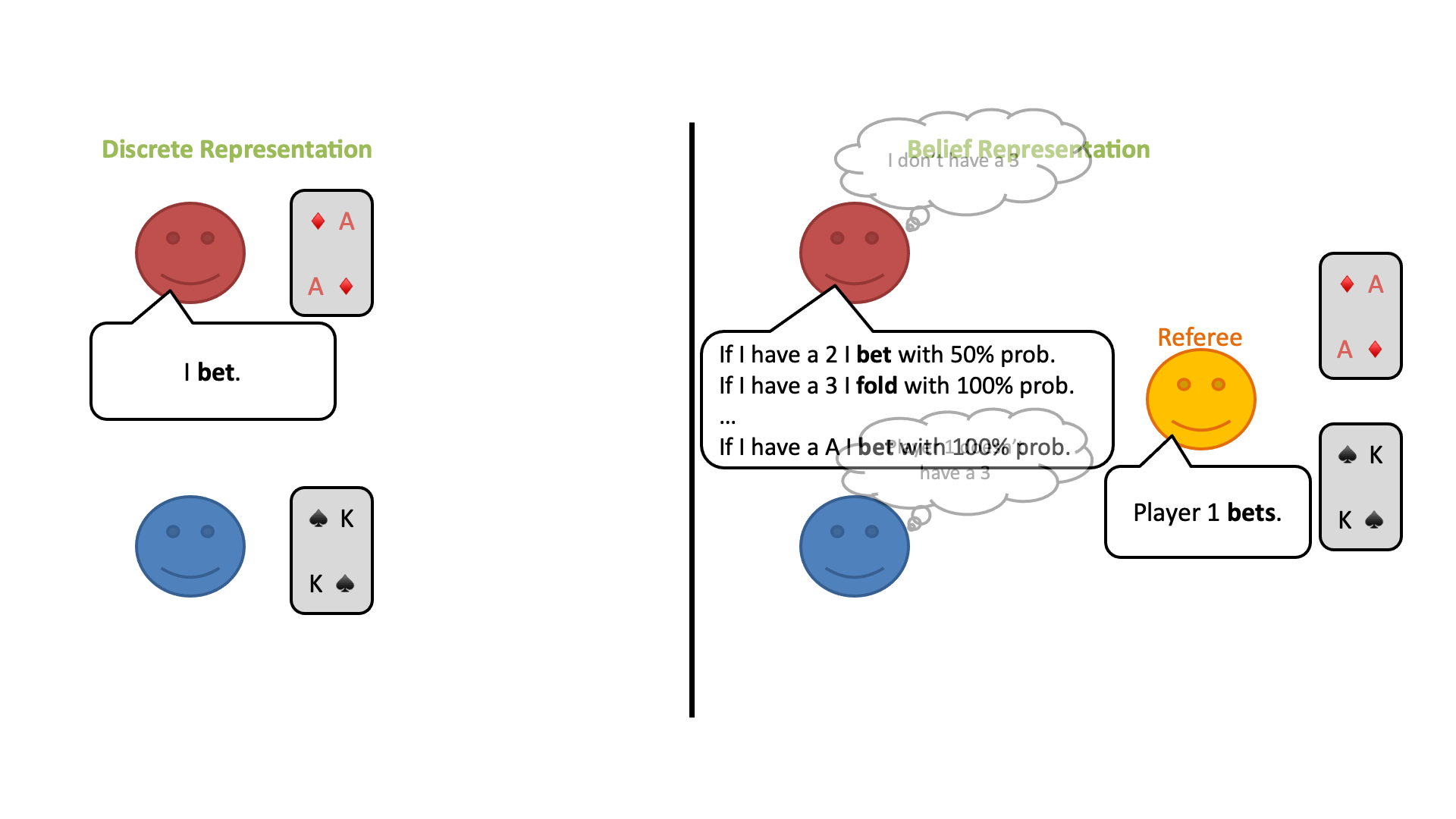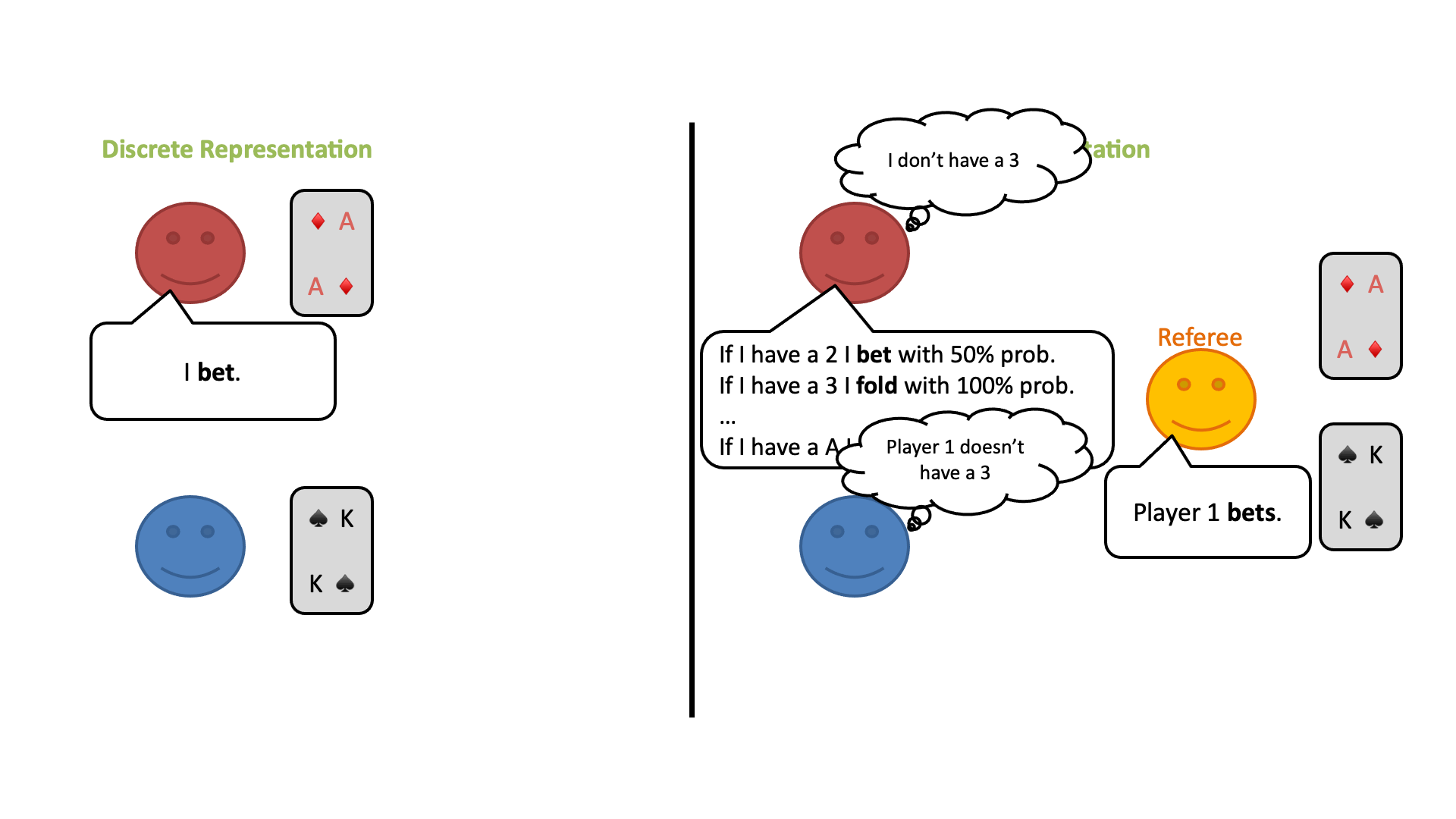
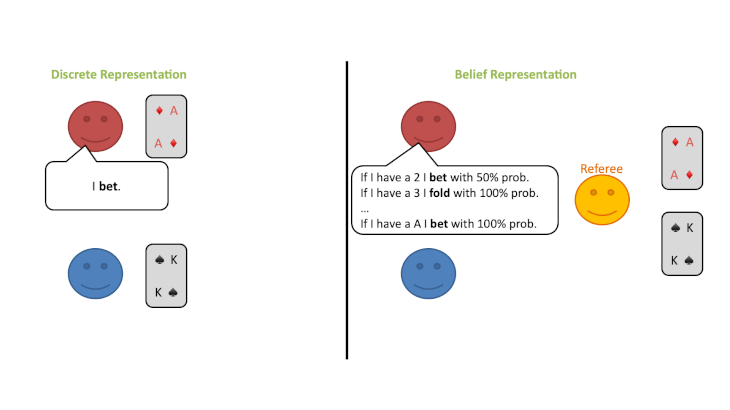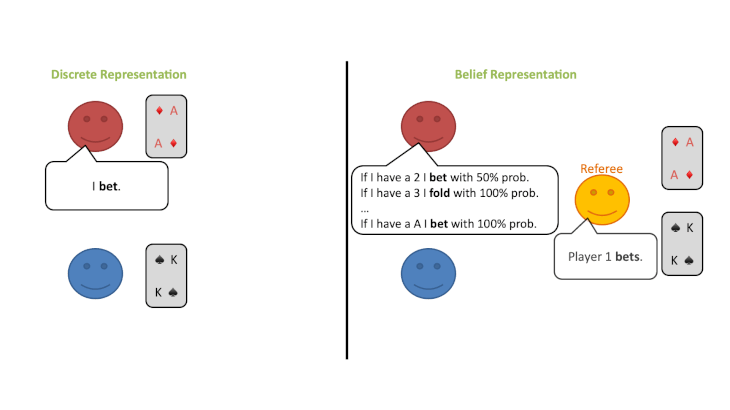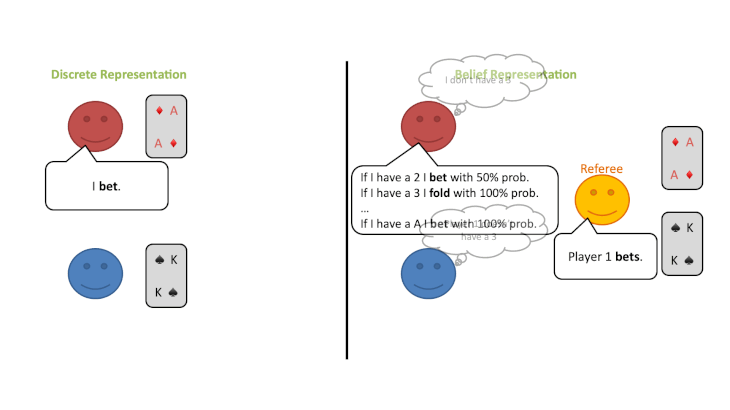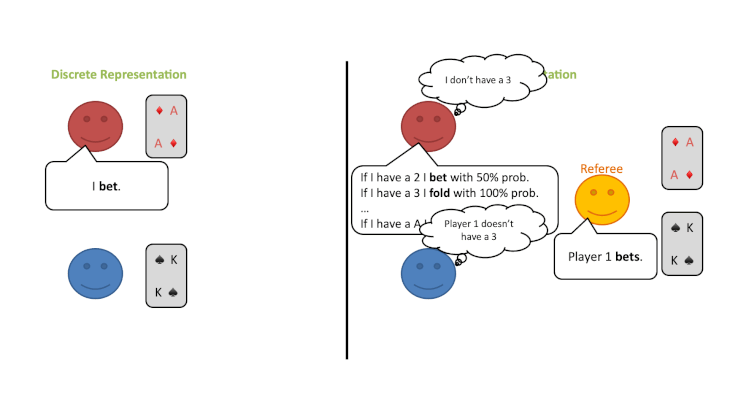
　この修正ゲームの開始時に、プレイヤーは自分のプライベートカードのすべての可能性についてランダムな信念分布を持っているとします。しかし、プレイヤーはラウンドごとに審判の行動から情報を得ることができ、何が起こったかに基づいてどのカードがプレイされている可能性があるかについての結論を導き出すことができます。
　ベイズの定理を使って、プレイヤーは自分のプライベートカードと相手のカードの両方について、信念分布を更新することができます。このようにして、各プレイヤーが特定のカードを持っている確率は、このゲームでは常にすべてのプレイヤーの間で共通の知識とすることができます。
　ここで重要なことは、このように考えると、この2つのゲーム（プレイヤーが自分のカードを見るゲームと、審判のみがすべてのカードを見るゲーム）は戦略的には同じであるが、後者のゲームはプライベートな情報を含まず（＝不完全情報状態ではない）、代わりに連続状態の完全情報ゲームであるということです。
　この発想自体は新しいわけではなく、長年研究が行われてきました。ReBeLはこの発想を強化学習と組み合わせたという点で新規性があります。
　このように不完全情報ゲームを完全情報ゲームに変換すると、原則として、AlphaZeroのようなモデルでも直接実行することができます。しかし、そのまま応用すると非常に非効率的であることが知られています。
　効率化するために、2人用のゼロサムゲームでは、高次元の状態空間とアクション空間は凸の最適化問題と扱います。そのため、ReBeLは、効率的な探索を行うために、CFR（counterfactual regret minimization）と呼ばれる勾配降下法に似たアルゴリズムを使用しています。
　ReBeLは、任意の2人用ゼロサムゲームにおいて、ナッシュ均衡に収束することが証明されています。

まとめ

　ReBeLははじめて効果的に不完全情報ゲームに対して、強化学習＋探索アルゴリズムモデルで対応することができるようになりました。しかし、実際に実用するにはまだまだ問題があることも指摘されています。
　ひとつは、計算量が多くなり、扱えないゲームも存在するということです。また、ゲームの正確なルールを知っていることにも依存しているため、現実世界のルールがはっきりしないゲーム状態では問題があります。
　しかし、それらを踏まえても非常に有効なモデルであることは事実であるため、今後の応用が期待されています。