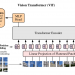
はじめに
MITがBERTなどの大規模なディープラーニングモデル内に、よりスリムで効率的なサブネットワークが存在することを発見しました。大規模モデルにはより有意義な小規模モデルが内包されているとする仮説「宝くじ仮説」(The Lottery Ticket Hypothesis)が指摘されています。今後、NLP分野における大規模モデルがより利用しやすくなることが期待されています。
Shrinking massive neural networks used to model language
https://news.mit.edu/2020/neural-model-language-1201
論文
The Lottery Ticket Hypothesis for Pre-trained BERT Networks
https://arxiv.org/abs/2007.12223
詳細
BERTなどの大規模ネットワークは、ほとんどのユーザーが利用することができない規模の計算資源を必要とします。そのため、一般のユーザーがBERTを使って学習させるといったことはほとんどありません。
しかし、今回の「宝くじ仮説」(The Lottery Ticket Hypothesis)の研究で大規模モデルにはよりスリムで効率的なサブネットワークが存在することが明らかにされました。(なお、この宝くじ仮説に関しては、同様の研究チームが2019年にICLRで発表した「THE LOTTERY TICKET HYPOTHESIS: FINDING SPARSE, TRAINABLE NEURAL NETWORKS」(https://openreview.net/pdf?id=rJl-b3RcF7)という論文で詳しく解説されています。)今後、多くのユーザーがモデルを利用した競争の場に参加することが可能になり、効果的なNLPツールが開発される可能性が指摘されています。
○背景
2018年にBERTが発表されて以来、NLP分野は大きく進歩しました。ただし、進歩の過程でパラメータの数も大きく上昇する傾向にあり、そのため計算コストも大きく上昇しています。標準的なBERTでも3憶4000万のパラメータを保有しており、最近のGPT-3などでは10憶にも達しています。このようなモデルになると、fine-tuningするだけでもスーパーコンピュータが必要となります。こうしたことが、一般の人々の参加障壁を高めていることを問題視し、モデルの省パラメータ化を目指したのが今回の研究になります。
○宝くじ仮説(The Lottery Ticket Hypothesis)
研究チームは、BERT内には無駄なパラメータで構成された部分が存在し、有意義なパラメータだけを保有しているサブネットワークがどこかに存在するという「宝くじ仮説」を検証しました。無駄なパラメータを破棄し、有意義なパラメータを発見することで性能を維持したまま小さなモデルを構築することを可能にします。
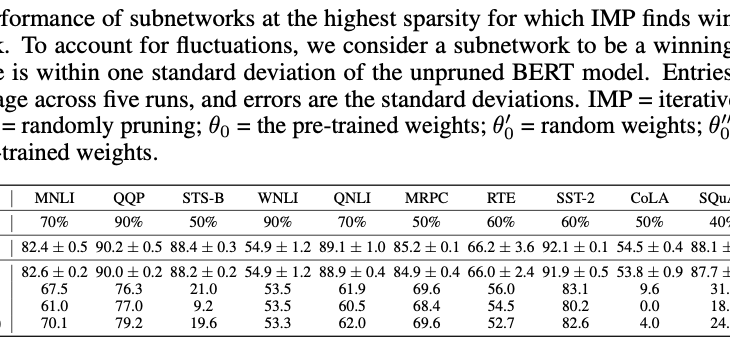
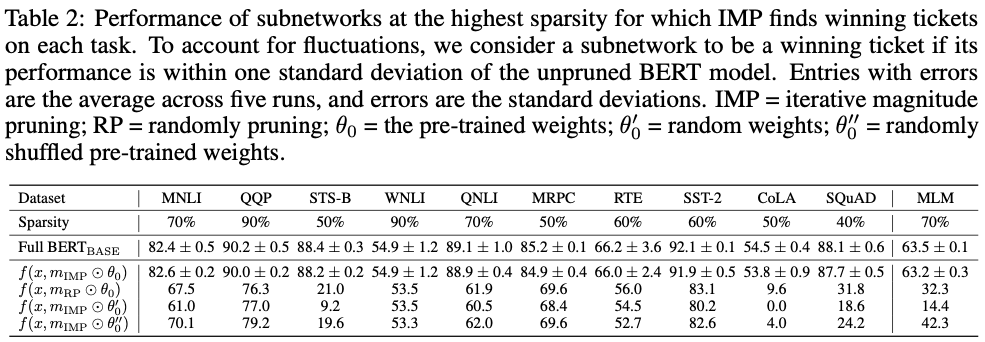
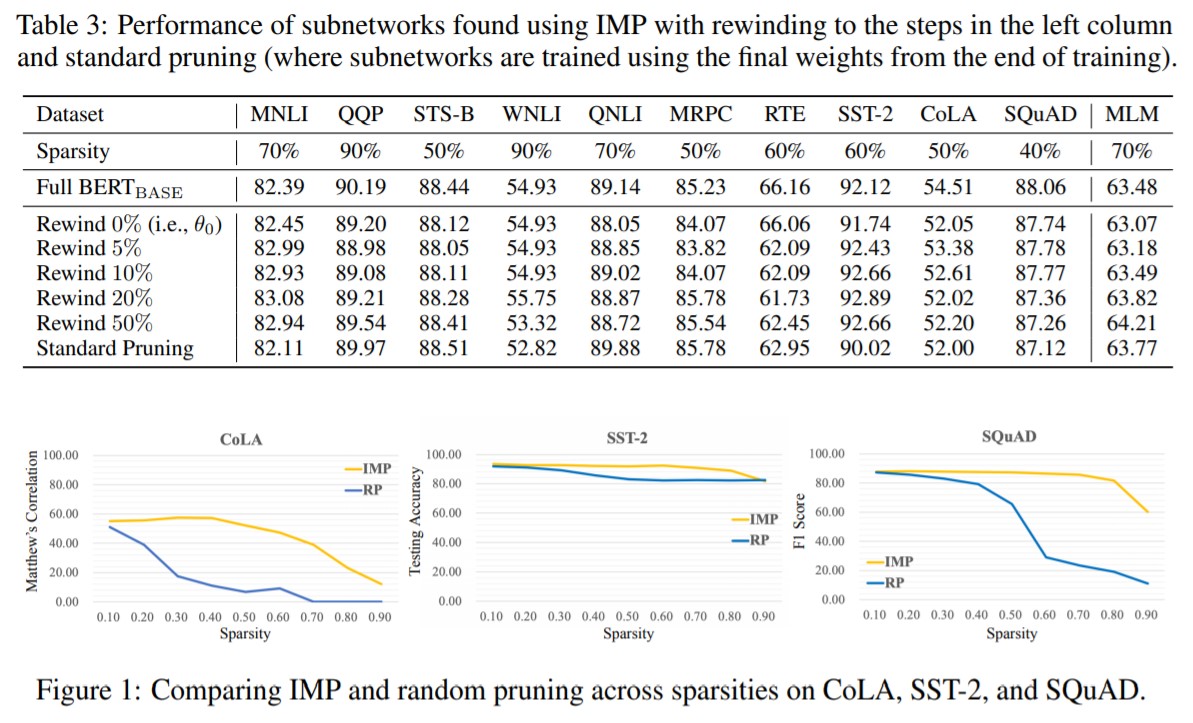
そのため、研究チームは、完全な状態のBERTからパラメータを繰り返しプルーニングし、新しいサブネットワークのパフォーマンスをもとのBERTと比較する実験を行いました。結果として、タスクに応じて同様の性能を発揮しながらも、40%~90%の省パラメータ化されたモデルを見つけることに成功しました。また、タスク固有のfine-tuningをするまえに、性能を発揮するモデルの特定をすることができたため、さらなる計算資源の効率化が可能になりました。
このことで、研究チームは「宝くじ仮説」にはある程度の説得力があると指摘しています。

○事前学習による初期化と転移学習について
・事前学習による初期化
大規模なモデルの設定では、宝くじ仮説は、ランダムな初期化ではなく、学習の初期の時点でしか一致するサブネットワークを見つけることができません。この時点以前では、これらのサブネットワークは、ランダムな剪定によって選択されたサブネットワークよりも良い性能を発揮しないことがわかっています。(この時点より前の学習の段階は、スパース化に適した初期化を作成する密度の高い事前訓練と見ることができます。)
・転移学習
宝くじ仮説を使ってマッチするサブネットワークを見つけるには、計算コストがかかるという問題があります。刈り込まれていないネットワークを最後まで学習し、不必要な重みを刈り込み、刈り込まれていない重みを学習の以前の値に巻き戻す必要があります。この行為の繰り返しは単にネットワーク全体を訓練するよりもコストが高くつきます。しかし、結果として得られるサブネットワークは、関連するタスク間で天気学習することができます。この特性により、サブネットワークを多くの異なる下流のタスクに再利用することができ、この宝くじを見つけるための計算資源への投資を正当化することが可能になります。
○研究成果
宝くじ仮説は、事前学習された BERT モデルの文脈ではまだ十分に理解されていません。今回の研究では、以下のような知見を得たとされています。
①構造化されていないマグニチュード・プルーニングを使用して、標準的なGLUEとSQuADの下流タスクのBERTモデルにおいて、40%から90%のスパース度でマッチング・サブネットワークを見つけることができました。
②NLPにおけるこれまでの研究とは異なり、これらのサブネットワークは、ある程度の学習後ではなく、(学習前の)初期化時に発見されることがわかりました。これまでの研究と同様に、これらのサブネットワークは、ランダムな剪定とランダムな再初期化によって発見されたサブネットワークよりも優れています。
③ほとんどの下流のタスクでは、これらのサブネットワークは他のタスクには移行しないので、マッチングするサブネットワークのスパースパリティパターンはタスク固有のものであることを意味します。
④マスクされた言語モデリングタスク(BERTの事前訓練に使用されるタスク)を使用して発見された、70%のスパース度のサブネットワークは普遍的であり、精度を維持しながら他のタスクに移行することができます。