FAIRが画像処理における解きほぐし手法の限界を発見！

はじめに
　FAIR（Facebook AI Research）が、自然の変化を捉えるために従来利用されている「disentanglement 解きほぐし」として知られるソリューションの限界を特定しました。

概要

　AIは自然界の多様性に対してうまく対応できないという問題は常に指摘されてきました。人間は、一度もみたことがないものでもそれまでの知識を利用することで、判断することができます。それに対して、AIは未知の状況を苦手にしています。こうした状況を解決するために、「解きほぐしdisentanglement 」として知られる手法がありますが、今回FAIRは解きほぐし手法の限界を特定しました。
　また、同変シフト演算子のアイデアを開発しました。これは、最も一般的な変換を模倣することでオブジェクトがどのように変化するかをモデルが理解するのに役立つ代替ソリューションの概念実証です。基本的には概念レベルであるものの、実験で精度の向上などが確認されました。

詳細

現在の「解きほぐし」手法

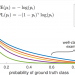
　「解きほぐし」は、データの変動要因を特定して区別することを目的としたもので、自然変動を特定するための既存のソリューションです。解きほぐしへの現在のアプローチは、モデルの内部表現における個別の部分空間に各要素をエンコードすることにより、モデル内のオブジェクトの基本的な変換を学習しようとします。（たとえば、解きほぐしによって、犬の画像のデータセットをポーズ、色、および品種の部分空間にエンコードします。）

　このアプローチは、単一のMNIST数字や椅子のような単一のオブジェクトクラスなど、厳密なデータセットの変動要因を特定するのに適していますが、複数のオブジェクトクラス間ではパフォーマンスが低いことがわかりました。
　これは三角形や正方形など、複数の回転する形状について考えることで理解できます。「解きほぐし」モデルは、変化の2つの要因、オブジェクトの形状と方向を2つの表現空間に分離しようとします。以下の画像は、従来の解きほぐしが複数の形状のデータセットの回転を分離できないことを示しています。ハイライトされた形状は回転すると予想されますが、解きほぐしに失敗したため、形状は固定されたままになります。

　「解きほぐし」はまた「位相の欠陥」をもたらします。位相の欠陥は連続性に違反します。連続性がないと、深層学習モデルはデータに存在するパターンを効果的に学習するのに苦労する可能性があります。

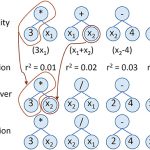
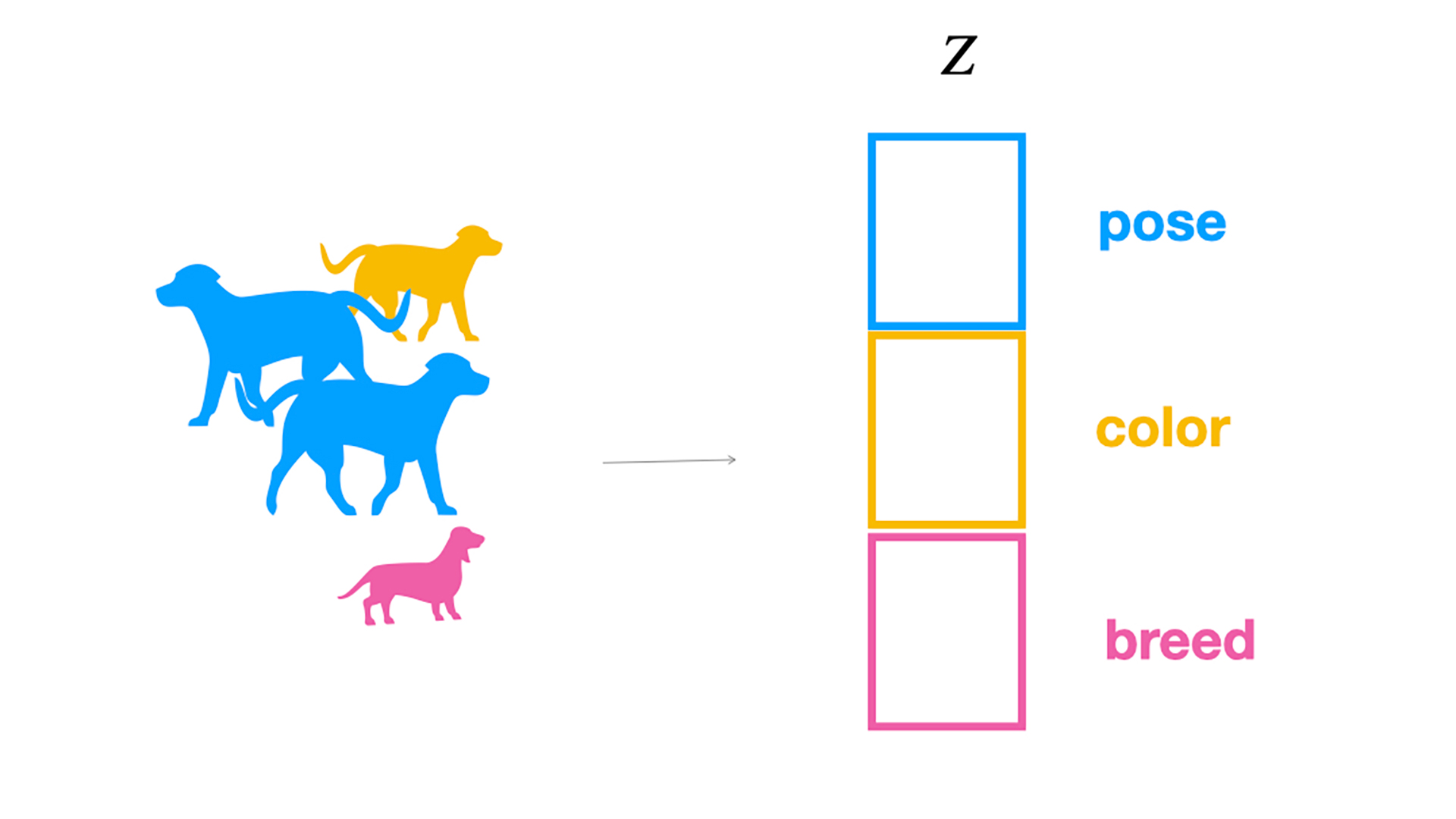
例えば、正三角形の回転を考えた場合、120度回転した正三角形は、元の三角形と区別がつかないため、方向空間で同じ表現になりますが、三角形の1つのコーナーに非常に小さなドットを追加すると、表現が区別可能になり、連続性に違反し、かなり離れた表現にマッピングされます。研究ではまた、位相欠陥が非対称形状や他の多くの一般的な変換で発生することを示しています。

同変演算子による変動の要因の発見

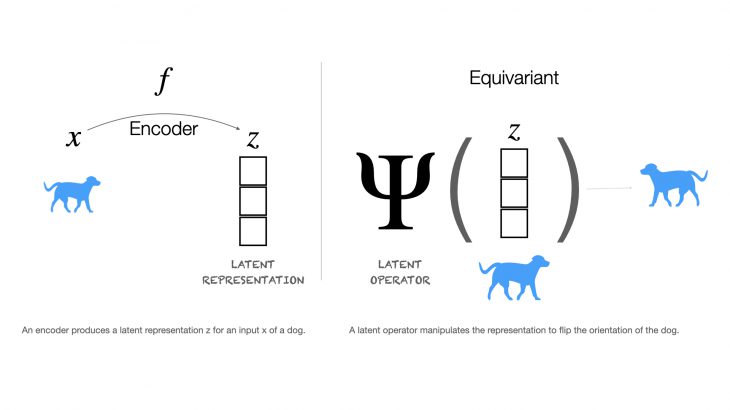
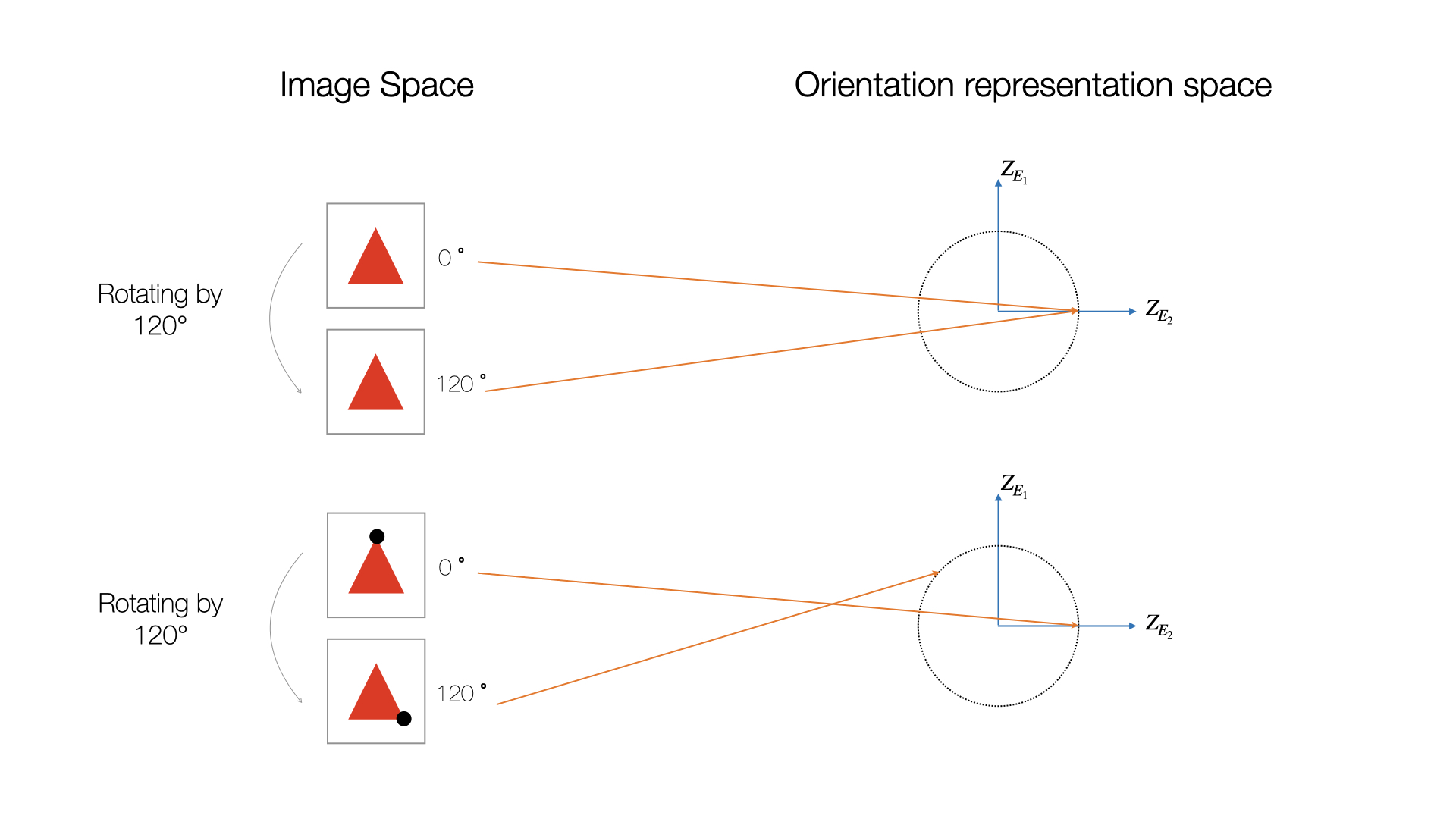
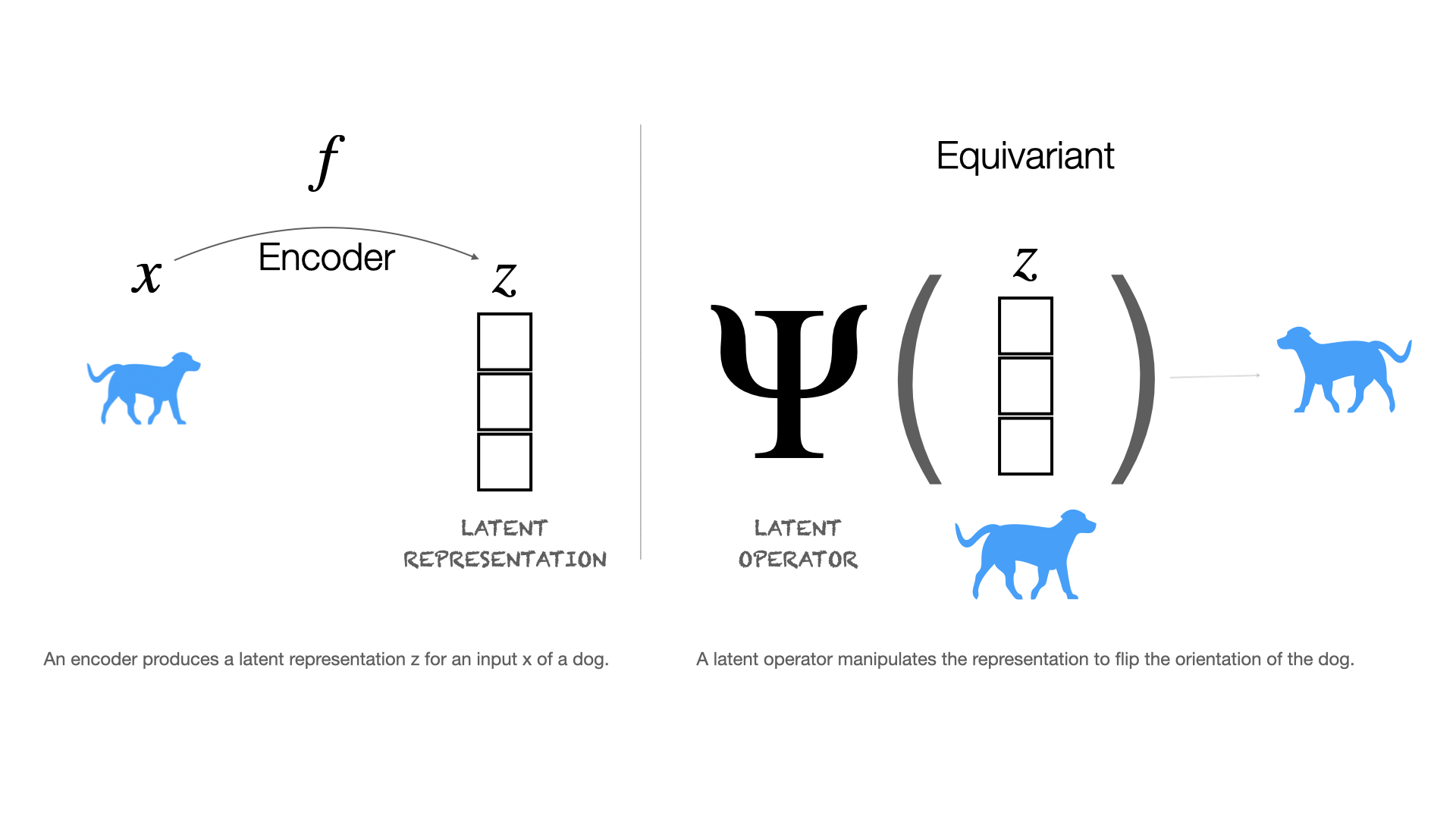
　各変換を表現の1つのコンポーネントに制限するのではなく、変換によって表現全体を変更できるとした場合、このアプローチの目標は、画像とその表現を操作できる演算子（変動の各要因に対して単一の演算子）を見つけることになります。これらは「同変 equivariant」として知られています。

　同変演算子の適用については、群論として知られる数学分野の知識が多くのヒントになります。これは、変動要因を理解する直感的な方法が、それらを変換のグループとしてモデル化することであることを示しています。たとえば、三角形の回転にはグループ構造があります。90度の回転と30度の回転を組み合わせて、120度の回転を生成します.

　これらのアイデアを使用して、従来の解きほぐしの欠点を特定し、同変演算子を解きほぐすようにトレーニングする方法を決定しました。シフト演算子と呼ばれる同変演算子を提案します。これは、一般的な変換（回転、平行移動、再スケーリング）のグループ構造を模倣するブロックを持つマトリックスです。元の画像とその変換の両方でAIモデルをトレーニングします。

　このことで、シフト演算子は、複数のクラスを含むデータセット間でも変換を正常に学習できることがわかりました。これは、従来の解きほぐしが通常失敗していた条件です。

まとめ

　群論に基づく同変モデルは解きほぐし研究の範囲を大幅に拡大しています。ただし、群論に基づくモデルで実際のデータセットに取り組むことは、困難が多く今後の課題となっています。