時系列データの予測モデルについて解説！

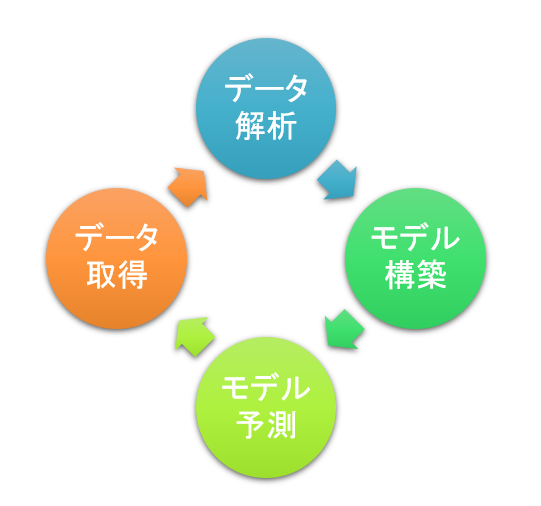
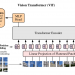
はじめに
　時系列データの予測モデルを構築し、データに合わせて最適化できるような標準化を行いました。今回は、時系列データの解析と予測モデルの構築方法についてご紹介します。

時系列データとは

　時系列データとは、「測定対象のある側面を一定の時間間隔で観測した結果の集合」のことです。連続量として扱うことができます。

例）毎日の気温や、営業日ごとの株価の終値

　
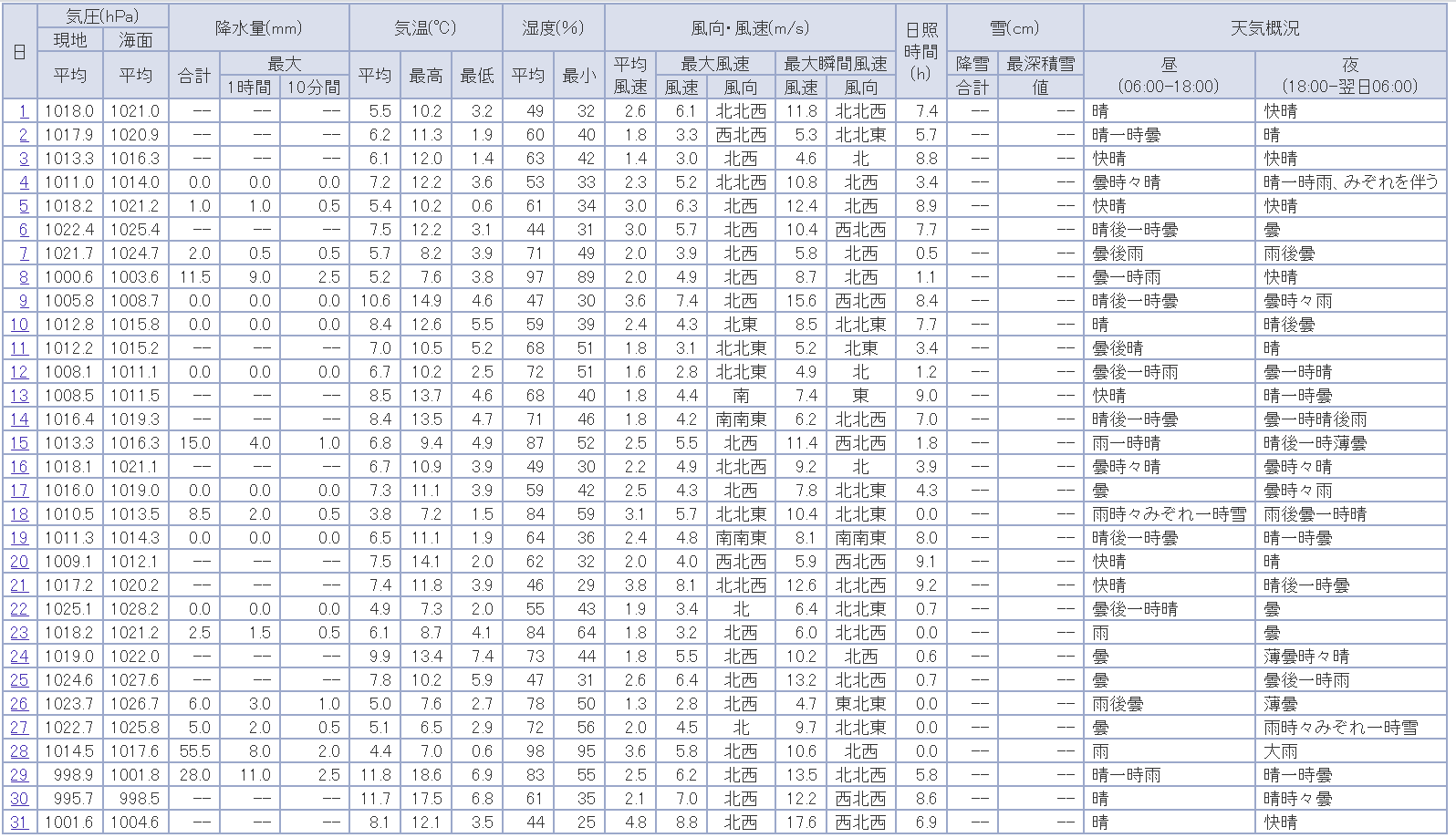
　なお、一定の間隔ではなく、事象が発生した時刻を持っているデータ（店舗の売上など）は、点過程データとよばれ、明確に区別されるので注意が必要です。

定常性の有無について

　時系列データは不規則な変動をしており、時系列解析ではこのような不規則な変動を確率的なモデルで表現することになります。
　その際、データの背後にある確率過程が時間変化に応じて変化しない場合（つまり安定している場合）、定常性がある（定常時系列である）といいます。この場合は、自己回帰型モデルを利用することができます。なお、　定常性には強弱があり、前提とする仮定が変化します。
　一方で、明確なトレンドがあったり、周期的に外的な影響が作用して、平均値や分散などが時間的に変化してしまう場合は、定常性がない（非定常時系列）といいます。

時系列データの構造について

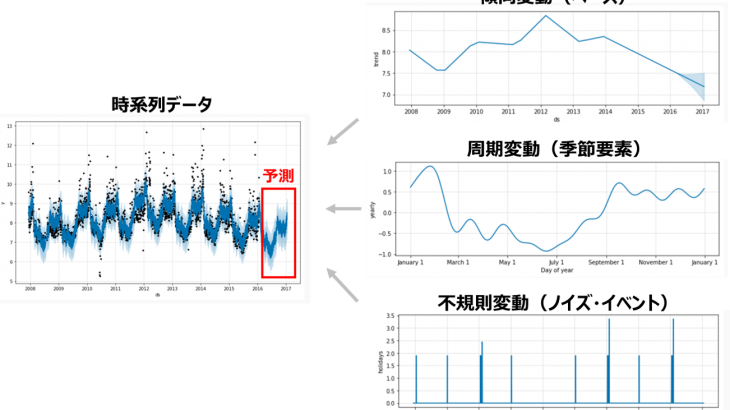
　時系列データは以下の三成分の合成であると考えることができます。

時系列データ＝傾向変動（トレンド）＋周期変動（季節変動）＋不規則変動（ノイズ）

●傾向変動（トレンド）：時間とともに単調に増加／減少する変動のこと。（長期的、系統的な変動であり、線形関数または非線形関数の形で表現される。）
●周期変動（季節変動）：単位時間で生じる周期（波の動き）変動のこと。
●不規則変動（ノイズ）：上記二つでは説明できない不規則かつ短期間に起こる変動のこと。

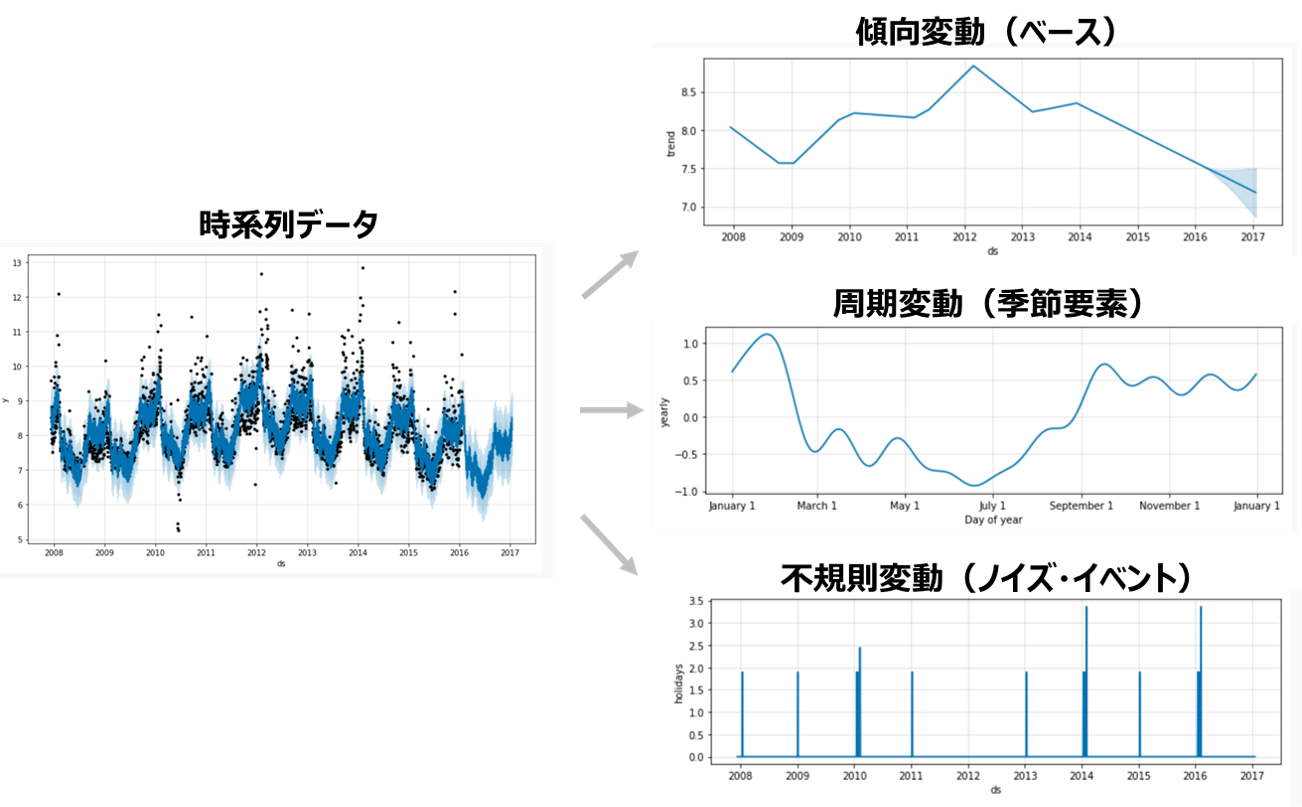
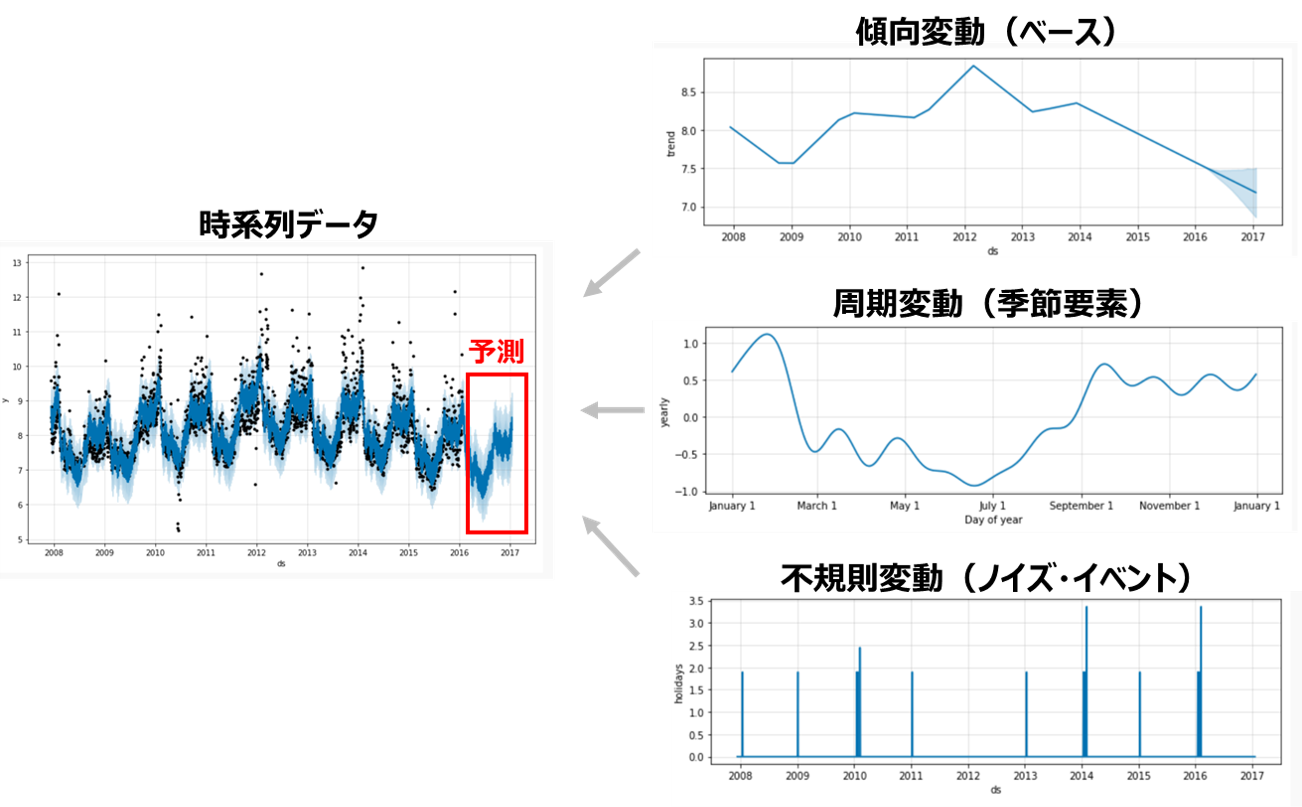
　これらの三成分を組み合わせることで予測モデルを構築します。時系列データをこれらの成分に分解して、可視化することで変動の仕方や影響の度合いなどを確認することもでき、より正確なモデルの構築につながります。

モデルの構築について

　時系列データを３つの基本成分の合成であると考える場合、合成の仕方には主に加法モデルと乗法モデルの二通あります。利用する時系列データの性質に合わせて、使い分ける必要があります。

①加法モデル
　時系列データ　＝　傾向変動（トレンド）＋周期変動（季節変動）＋不規則変動（ノイズ）

②乗法モデル
　時系列データ　＝　傾向変動（トレンド）×周期変動（季節変動）×不規則変動（ノイズ）

　一般に、傾向変動の大きさと周期変動の振れ幅に相関がある場合、乗法モデルの方がうまくあてはまるといわれています。

まとめ

　ここまで主に「データ解析」と「モデル構築」について概念的に説明しました。
　データを解析し、モデルを構築するだけではあまり意味がありません。解析後にモデルから予測をだすことではじめて行動の指針となります。そして、予測値と実際値を比較することで、モデルの問題点やデータ内のとらえきれていない特徴を洗い出し、さらに精度のよいモデルを構築することが可能となります。実際のモデルの構築から更新までの流れは「【実例紹介】時系列データを誰でも利用できるようにフォーマット化しました」をご参照ください。